Top 10 công thức hình học trong chương trình tiểu học và bài tập có liên quan chi tiết nhất
Các công thức hình học ở bậc tiểu học mà các em học sinh cần ghi nhớ: công thức tính chiều dài, chiều cao, chu vi, diện tích của các hình tam giác, vuông… Mong...xem thêm ...
Hình Vuông
Hình vuông là 1 hình tứ giác có 4 cạnh bằng nhau và 4 góc bằng nhau. Hình vuông có đầy đủ các tính chất của 1 hình chữ nhật, hình thoi và hình thang. Hình vuông có 4 góc vuông, đường chéo vuông góc tại trung diểm, 2 cặp cạnh đối song song với nhau.
Các công thức tính:
- Chu vi hình vuông: 𝑷 = 𝒂 × 4 (cùng đơn vị đo)
- Cạnh: 𝒂 = 𝑷 : 4
- Diện tích hình vuông: 𝑺 = 𝒂 × 𝒂 (cùng đơn vị đo).
Chú ý:
- Trong hình vuông nếu tăng 1 cạnh lên a đơn vị thì chu vi sẽ tăng 4 x a đơn vị.
- Trong hình vuông nếu cạnh tăng lên a lần thì diện tích sẽ tăng lên a x a lần.
Bài tập về hình vuông:
Bài 1: Một hình vuông có chu vi 32 cm. Hỏi diện tích của hình vuông đó bằng bao nhiêu?
Lời giải:
- Cạnh của hình vuông là: 32 : 4 = 8 (cm).
- Diện tích hình vuông là: 8 x 8 = 64 (cm2)
- Đáp số: 64 (cm2)
Bài 2: Một miếng đất hình vuông, sau khi mở rộng về một phía thêm 8m thì được một hình chữ nhật có chu vi 116m. Hỏi sau khi mở rộng, miếng đất có diện tích là bao nhiêu?
Lời giải:
- Chu vi miếng đất hình vuông là:
- 116 – 8 x 2 = 100 (m)
- Cạnh của miếng đất hình vuông (cũng là chiều rộng của hình chữ nhật) là:
- 100 : 4 = 25 (m)
- Chiều dài miếng đất hình chữ nhật là:
- 25 + 8 = 33 (m)
- Sau khi mở rộng, miếng đất có diện tích là:
- 25 x 33 = 825 (m2)
- Đáp số: 825 (m2)
Bài 3: Tìm diện tích miếng đất hình vuông, biết rằng khi mở rộng mỗi cạnh của miếng đất thêm 4 m thì diện tích tăng thêm 224
Lời giải:
- Phần diện tích tăng thêm là diện tích của hình chữ nhật có chiều rộng 4 m, chiều dài bằng 2 lần cạnh hình vuông và cộng thêm 4 m.
- Chiều dài của hình chữ nhật nói trên là:
- 224 : 4 = 56 (m)
- Hai lần cạnh miếng đất hình vuông bằng:
- 56 – 4 = 52 (m)
- Cạnh miếng đất hình vuông bằng:
- 52 : 2 = 26 (m)
- Diện tích miếng đất hình vuông bằng:
- 26 x 26 = 676 (m2)
- Đáp số: 676 (m2)

Hình chữ nhật
Hình chữ nhật là tứ giác có bốn góc vuông. Tứ giác ABCD là hình chữ nhật. Có bốn góc A, B, C, D bằng 90 độ
Chú ý: Hình chữ nhật cũng là một hình bình hành, hình thang cân.
Các công thức tính:
- Chu vi: P = (a + b) x 2 (P: chu vi)
- Chiều dài: a = P/2 - b (a: chiều dài)
- Chiều rộng: b = P/2 - a (b: chiều rộng)
- Diện tích: S = a x b (S: diện tích)
- Chiều dài: a = S : b
- Chiều rộng: b = S : a
Bài tập về hình chữ nhật:
1. Bài tập về tính chu vi hình chữ nhật, diện tích hình chữ nhật
Bài 1: Tính chu vi và diện tích của hình chữ nhật có chiều rộng bằng 20cm và chiều dài bằng 25cm?
Lời giải:
- Chu vi của hình chữ nhật là:
- (20 + 25) x 2 = 90 (cm)
- Diện tích của hình chữ nhật là:
- 20 x 25 = 500 (cm2)
- Đáp số: 90cm và 500cm2
Bài 2: Tính chu vi và diện tích của hình chữ nhật có chiều rộng bằng 15cm và nửa chu vi bằng 40cm?
Lời giải:
- Chu vi của hình chữ nhật là:
- 40 x 2 = 80 (cm)
- Chiều dài của hình chữ nhật là:
- 40 - 15 = 25 (cm)
- Diện tích của hình chữ nhật là:
- 15 x 25 = 375 (cm2)
- Đáp số: 80cm và 375cm2
2. Bài luyện tập tính chu vi, diện tích hình chữ nhật
Bài 1: Một hình chữ nhật có chu vi 72 cm. Nếu giảm chiều rộng đi 6cm và giữ nguyên chiều dài thì diện tích giảm đi 120 cm2.
Tính chiều dài và chiều rộng hình chữ nhật đó.
Bài 2: Một mảnh đất hình chữ nhật có chiều dài 14 m. Nếu chiều rộng tăng 2 m, chiều dài giảm 3m thì mảnh đất đó trở thành hình vuông. Tính chu vi mảnh đất đó.
Bài 3: Một mảnh đất hình chữ nhật có chiều dài 12 m, biết rằng 3 lần chiều rộng thì bằng 2 lần chiều dài. Tính chu vi mảnh đất đó.
Bài 4: Nếu bớt một cạnh hình vuông đi 4 cm thì được hình chữ nhật có diện tích kém diện tích hình vuông 60 cm2. Tính chu vi hình vuông đó.
Bài 5: Một hình vuông có chu vi là 24 cm. Một hình chữ nhật có chiều rộng bằng cạnh của hình vuông và biết 3 lần cạnh hình vuông thì bằng 2 lần chiều dài hình chữ nhật. Tính diện tích mỗi hình đó.
Bài 6: Biết chu vi một hình chữ nhật gấp 6 lần chiều rộng. Hỏi chiều dài hình chữ nhật đó gấp mấy lần chiều rộng?
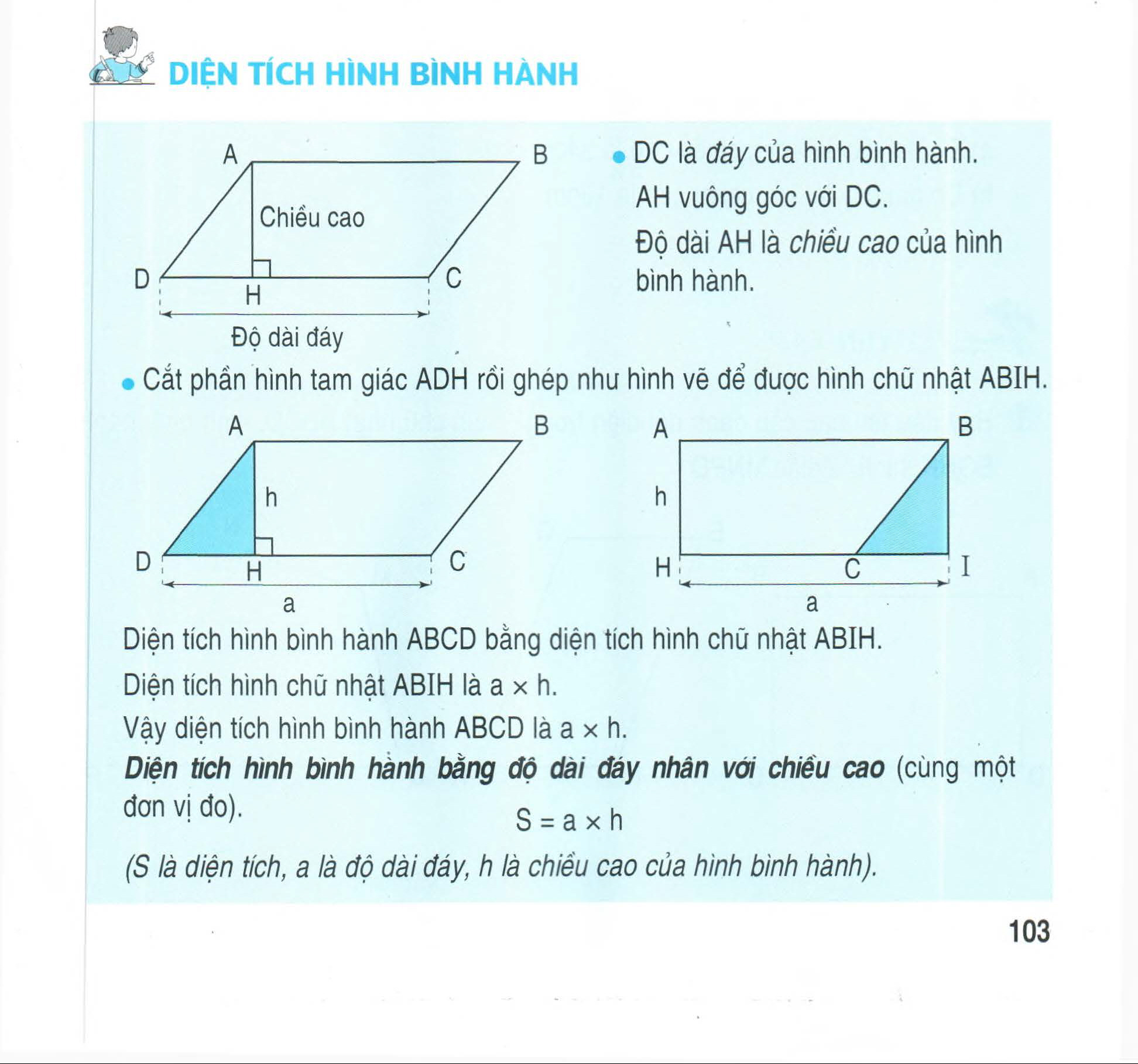
Hình bình hành
Hình bình hành là tứ giác mà có 2 cặp cạnh đối song song với nhau hoặc 1 cặp cạnh đối song song và bằng nhau. Trong hình bình hành có 2 góc đối bằng nhau; 2 đường chéo sẽ cắt nhau tại trung điểm của hình. Dễ nhớ hơn có thể hiểu hình bình hành là 1 trường hợp đặc biệt của hình thang.
Công thức tính:
- Chu vi: P = (a + b) x 2 (a: độ dài đáy)
- Diện tích: S = a x h (b: cạnh bên)
- Diện tích: S = a x h (h: chiều cao)
- Độ dài đáy: a = S : h
- Chiều cao: h = S : a
Bài tập về hình bình hành:
Bài tập 1:
Cho hình bình hành ABCD có chiều cao hạ xuống cạnh CD là 5, chiều dài CD là 15, hãy tính diện tích hình bình hành ABCD
Bài giải:
- S (ABCD) = 5 x 15 = 75 cm2
Bài tập 2:
Mảnh đất hình bình hành có cạnh đáy là 47m, mở rộng mảnh đất bằng cách tăng các cạnh đáy của hình bình hành này thêm 7m thì được mảnh đất hình bình hành mới có diện tích hơn diện tích mảnh đất ban đầu là 189m2. hãy tính diện tích mảnh đất ban đầu.
Bài giải:
- Phần diện tích tăng thêm chính là diện tích hình bình hành có cạnh đáy 7m và chiều cao là chiều cao của mảnh đất hình bình hành ban đầu.
- Chiều cao mảnh đất là: 189 : 7 = 27 (m)
- Diện tích mảnh đất hình bình hành ban đầu là: 27 x 47 = 1269 (m2)
Bài tập 3:
Cho hình bình hành có chu vi là 480cm, có độ dài cạnh đáy gấp 5 lần cạnh kia và gấp 8 lần chiều cao. Tính diện tích hình bình hành
Bài giải:
- - Ta có nửa chu vi hình bình hành là: 480 : 2 = 240 (cm)
- - Nếu như coi cạnh kia là 1 phần thì cạnh đáy chính là 5 phần như vậy.
- Ta có cạnh đáy hình bình hành là: 240 : (5+1) x 5 = 200 (cm)
- Tính được chiều cao của hình bình hành là: 200 : 8 = 25 (cm)
- Diện tích của hình bình hành là: 200 x 25 = 5000 (cm2)
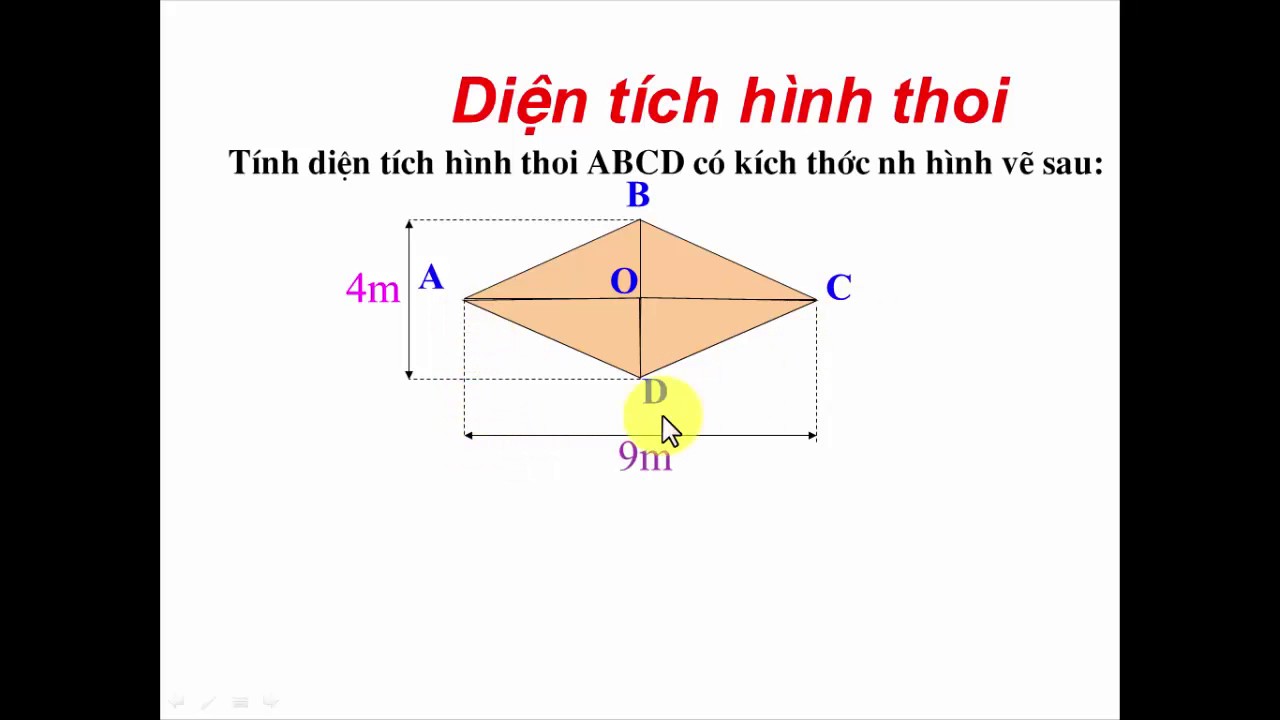
Hình thoi
Hình thoi là hình tứ giác có 4 cạnh bằng nhau và có một số tính chất như: 2 góc đối bằng nhau, 2 đường chéo vuông góc với nhau và cắt tại trung điểm của mỗi đường đồng thời là đường phân giác của các góc. Hình thoi có đầy đủ các tính chất của hình bình hành.
Công thức tính:
- Diện tích: S = (m x n) : 2 (m: đường chéo thứ nhất)
- Tích 2 đường chéo: (m x n) = S x 2 (n: đường chéo thứ nhất)
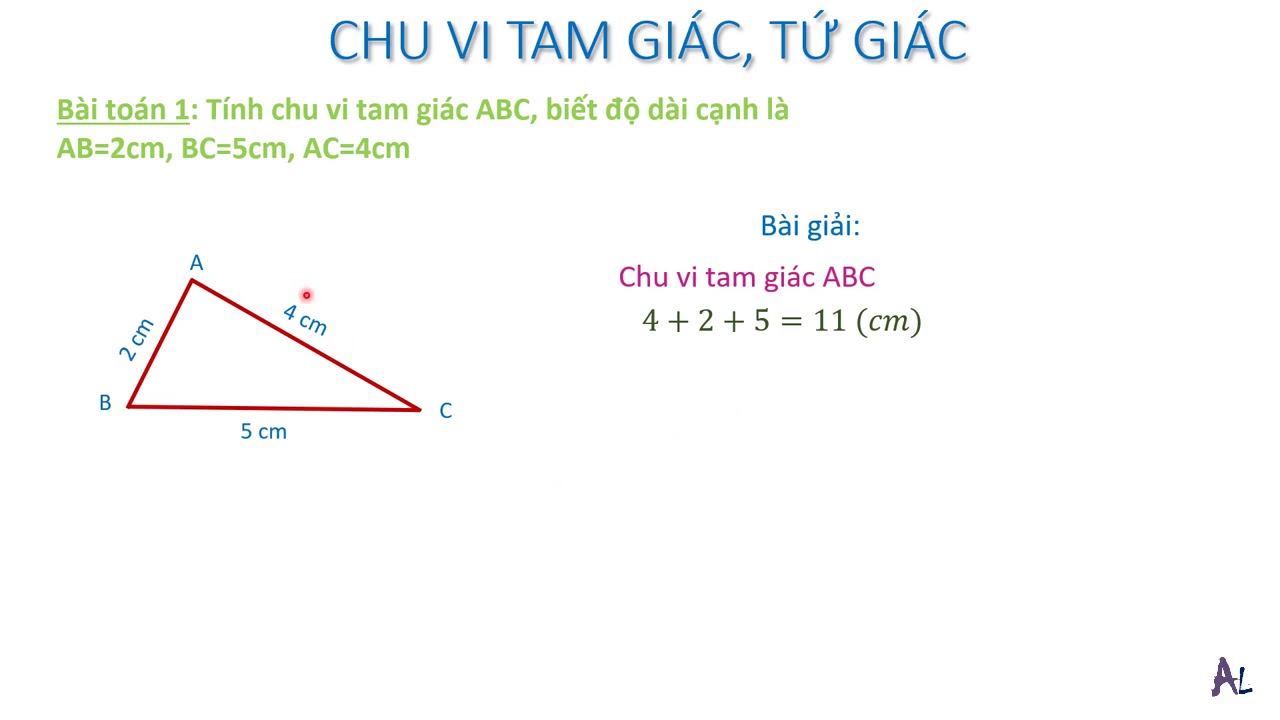
Hình tam giác
Tam giác hay hình tam giác là một loại hình cơ bản trong hình học: hình hai chiều phẳng có ba đỉnh là ba điểm không thẳng hàng và ba cạnh là ba đoạn thẳng nối các đỉnh với nhau. Tam giác là đa giác có số cạnh ít nhất (3 cạnh). Tam giác luôn luôn là một đa giác đơn và luôn là một đa giác lồi (các góc trong luôn nhỏ hơn 180o).
Công thức tính:
- Chu vi: P = a + b + c (a: cạnh thứ nhất; b: cạnh thứ hai; c: cạnh thứ ba)
- Diện tích: S = (a x h) : 2 (a: cạnh đáy)
- Chiều cao: h = (S x 2) : a (h: chiều cao)
- Cạnh đáy: a = (S x 2) : h
Hình tam giác vuông
Diện tích: S = (a x a) : 2
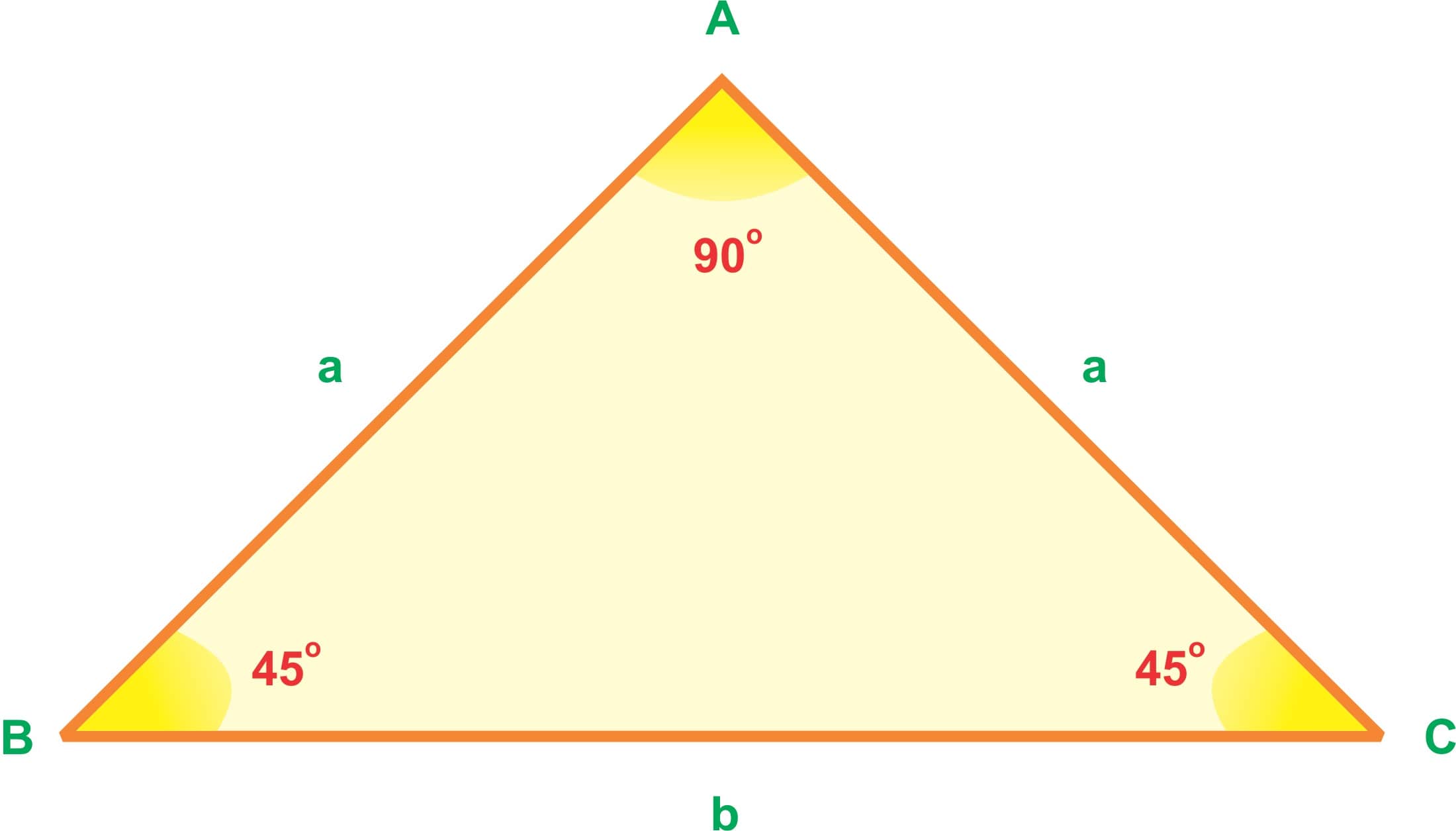
Công thức tính hình thang
Hình thang là một tứ giác lồi có 2 cạnh đối song song. Hai cạnh này được gọi là hai cạnh đáy của hình thang. Hai cạnh còn lại là hai cạnh bên.
Các trường hợp đặc biệt của hình thang:
- Hình thang vuông: Hình thang có 1 góc vuông được gọi là hình thang vuông
- Hình thang cân: Hình thang có 2 góc kề một cạnh đáy bằng nhau là hình thang cân.
- Hình thang vuông cân: Là hình thang vừa vuông vừa cân và còn được gọi là hình chữ nhật.
Công thức tính hình thang:
- Diện tích: S = (a + b) x h : 2 (a & b: cạnh đáy)
- Chiều cao: h = (S x 2) : a (h: chiều cao)
- Cạnh đáy: a = (S x 2) : h
- Chu vi hình thang: Muốn tìm chu vi hình thang ta lấy tổng chiều dài hai cạnh bên và hai cạnh đáy: P = a + b + c + d
- Tổng chiều dài hai đáy hình thang: Muốn tìm tổng chiều dài hai đáy hình thang, ta lấy hai lần diện tích chia cho chiều cao.
- Muốn tìm đáy lớn, (đáy bé) hình thang ta lấy tổng hai đáy trừ đi đáy bé (đáy lớn)

Công thức tính hình tròn
Trong hình học phẳng, một hình tròn là một vùng trên mặt phẳng nằm "bên trong" đường tròn. Tâm, bán kính và chu vi của hình tròn chính là tâm và bán kính của đường tròn bao quanh nó.
Một hình tròn được gọi là đóng hay mở tùy theo việc nó chứa hay không chứa đường tròn biên.
Công thức tính hình tròn:
- Bán kính hình tròn: r = d : 2 hoặc r = C : 2 : 3,14
- Đường kính hình tròn: d = r x 2 hoặc d = C : 3,14
- Chu vi hình tròn: C = r x 2 x 3,14 hoặc C = d x 3,14
- Diện tích hình tròn: C = r x r x 3,14
- Tìm diện tích thành giếng:
- Tìm diện tích miệng giếng: S = r x r x 3,14
- Bán kính hình tròn lớn = bán kính hình tròn nhỏ + chiều rộng thành giếng
- Diện tích hình tròn lớn: S = r x r x 3,14
- Tìm diện tích thành giếng = diện tích hình tròn lớn - diện tích hình tròn nhỏ

Công thức tính hình hộp chữ nhật
- Diện tích xung quanh: Sxq = Pđáy x h
- Chu vi đáy: Pđáy = Sxq : h
- Chiều cao: h = Sxq : P đáy
- Nếu đáy của hình hộp chữ nhật là hình chữ nhật thì:
Pđáy = (a + b) x 2
- Nếu đáy của hình hộp chữ nhật là hình vuông thì:
Pđáy = a x 4
- Diện tích toàn phần: Stp = Sxq + S2đáy
Sđáy = a x b
- Thể tích: V = a x b x c
- Muốn tìm chiều cao cả hồ nước (bể nước)
h = v : Sđáy
- Muốn tìm diện tích đáy của hồ nước (bể nước)
Sđáy = v : h
- Muốn tìm chiều cao mặt nước đang có trong hồ ta lấy thể tích nước đang có trong hồ (m3) chia cho diện tích đáy hồ (m2)
h = v : Sđáyhồ
- Muốn tìm chiều cao mặt nước cách miệng hồ (bể) (hay còn gọi là chiều cao phần hồ trống)
+ Bước 1: Ta tìm chiều cao mặt nước đang có trong hồ.
+ Bước 2: Lấy chiều cao cả cái hồ trừ đi chiều cao mặt nước đang có trong hồ
Diện tích quét vôi:
- Bước 1: Chu vi đáy căn phòng.
Bước 2: Diện tích bốn bức tường (Sxq)
Bước 3: Diện tích trần nhà (S = a x b)
Bước 4: Diện tích bốn bức tường (Sxq) và trần nhà
Bước 5: Diện tích các cửa (nếu có)
Bước 6: Diện tích quét vôi = diện tích bốn bức tường và trần – diện tích các cửa.

Công thức tính hình lập phương
- Diện tích xung quanh: Muốn tìm diện tích xung quanh của hình lập phương ta lấy cạnh nhân với cạnh rồi nhân với 4: Sxq = (a x a) x 4
- Cạnh: (a x a) = Sxq : 4
- Diện tích toàn phần: Muốn tìm diện tích toàn phần của hình lập phương ta lấy cạnh nhân với cạnh rồi nhân với 6: Stp = (a x a) x 6
- Cạnh: (a x a) = Stp : 6
- Thể tích ( V ): Muốn tìm thể tích hình lập phương ta lấy cạnh nhân với cạnh rồi nhân với cạnh: V = a x a x a

Hãy đăng nhập để bình luận
Đăng nhập bằng facebook hoặc google để bình luận .




